画像をダウンロード 三平方の定理 ルートの計算 122458-三平方の定理 ルート の計算

三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学

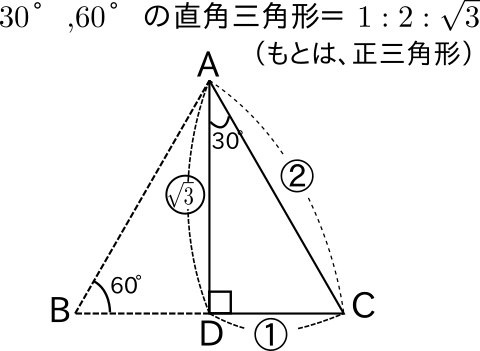
 これらの形を暗記すると、よりスピーディに計算できるようになります。 もちろん、万が一それぞれの辺の比を忘れてしまっても、直角三角形の \(2\) 辺の長さがわかっていれば、もう \(1\) 辺の長さは三平方の定理で導き出せるので、あわてないでくださいね。三平方の定理 発展問題まとめ お疲れ様でした！ 入試などの発展問題では、今回のように 三平方の定理を使って、方程式を作ることで 長さを求めていくようになります。 まずは、求めたい部分を とする。 直角三角形の各辺を を使って表すことが

三平方の定理 ルートの計算

三平方の定理 ルートの計算- 三角比とは、形を変えた三平方の定理といえます。 三平方の定理をもう少しわかりやすく、使いやすくするためにサインとコサインという道具があります。中学と高校でやっていることは本質的に同じと考えられます。 中学 → 三平方の定理 高校 → 三角比約6年前 a^2＋b^2=c^2を等式変形すれば√ (a^2＋b^2)=cとなるからです。 x^2=9でx=±√9と同じです この回答にコメントする コン 約6年前 三平方の定理をそのまま使ったら BD^2が求まるので最後に√をかけてBDを求めますよね。 それを最初からいっぺんにやって

ピタゴラスの定理 Wikipedia

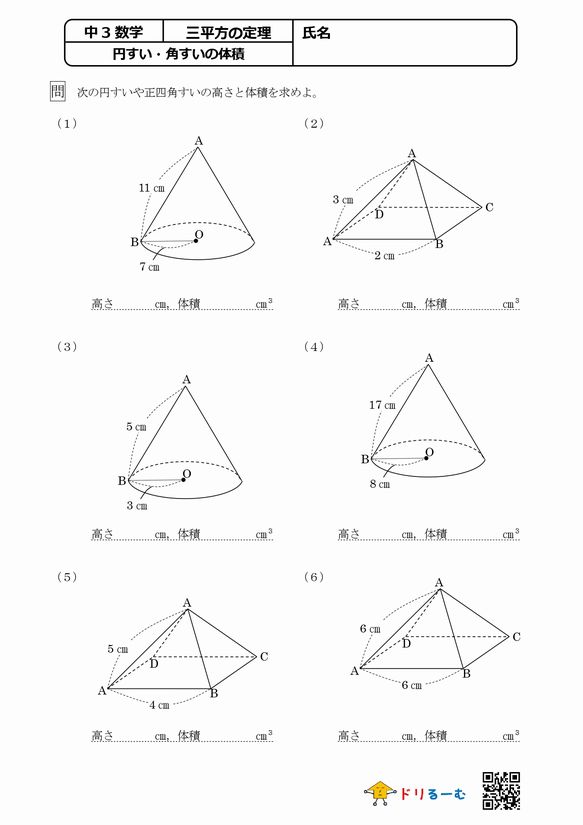
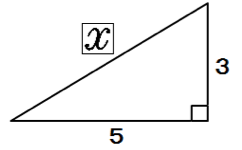
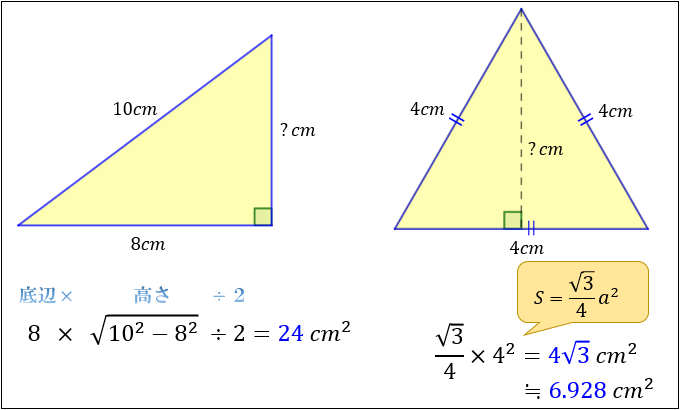
 三平方の定理（基礎） 直角三角形で2辺の長さがわかれば三平方の定理でもう1辺の長さが出ます。 定理に当てはめて計算するだけですが、ルートの計算を慎重に行ってくださいね。 今回は基本ですが、しっかり練習して慣れましょう。 三平方の定理の特別三角形の1対1対ルート2と1対2対ルート3の意味がわからないので わかるかたは教えてください 高校 締切済 教えて！goo 三平方の定理を使って三角形の計算をします。 かんたん計算機 三平方の定理 計算機 「ご注意計算結果について、正確な結果が出るように検証をしていますが、間違いがある可能性も

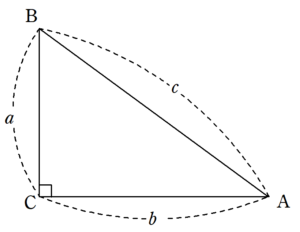
 ルートの計算（基礎） 中3数学 ルートは2乗がポイントとなります。 2乗のものはルートの外に出さないといけません。 最初は素因数分解でいいですが、いずれはそれをしなくてもすぐにルートを簡単にできるよう、覚えるまで問題を解き 三平方の定理とは 三平方の定理とは,直角三角形において各辺の関係は 斜辺 2 ＝ 底辺 2 ＋ 高さ 2 となる定理のことで、この定理のおかげで、 2辺の長さが分かればあと1辺の長さを求めることができる。三平方の定理の解説 直角三角形における3辺の長さによる定理を 三平方の定理 (さんへいほうのていり)と言います。 ピタゴラスの定理とも言われます。 三平方の定理では、直角三角形の斜辺をc、その他の辺をそれぞれa、bとした場合に、 a 2 b 2 = c 2 が成り立ちます。

三平方の定理 ルートの計算のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	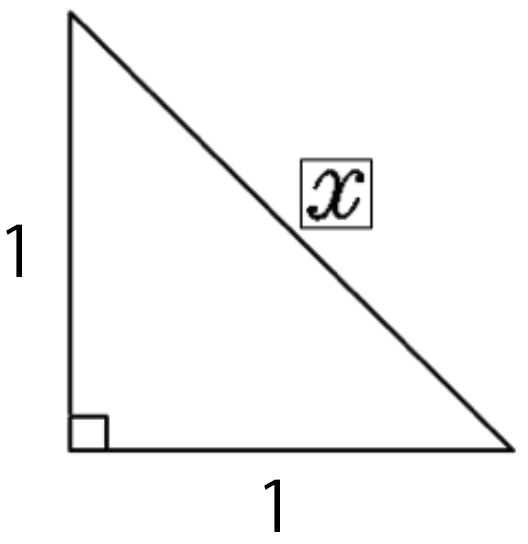三平方の定理 練習問題 苦手な数学を簡単に	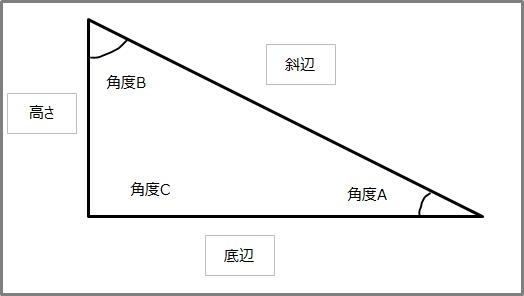三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に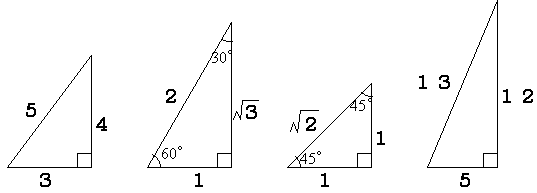
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	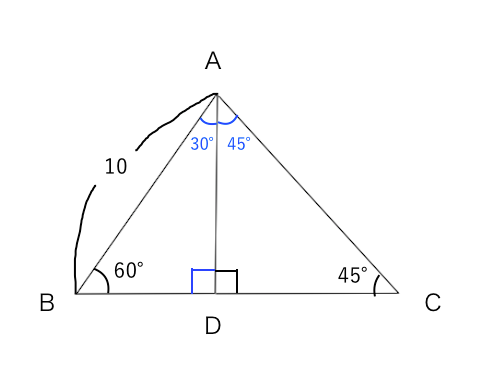三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	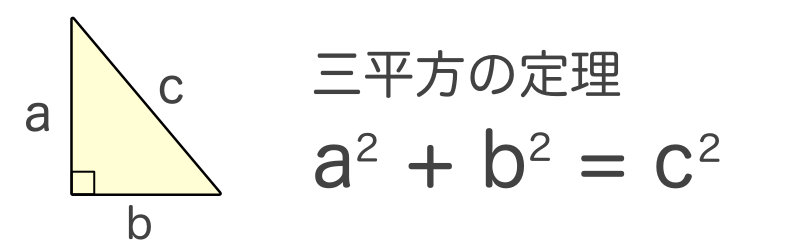三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に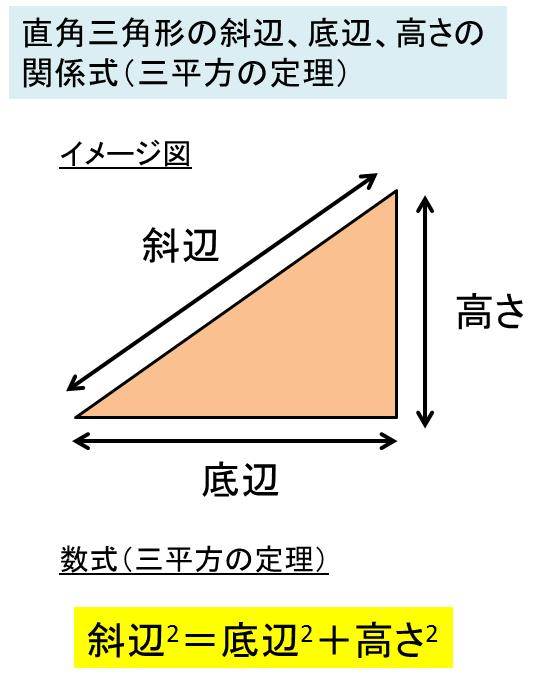
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	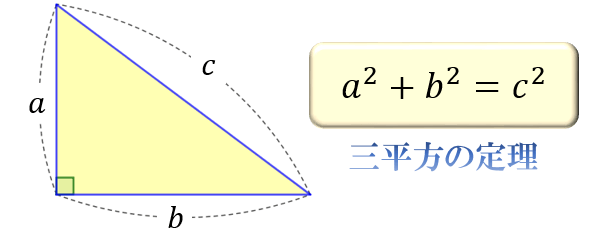三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に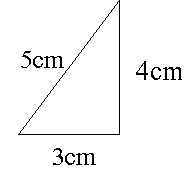
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	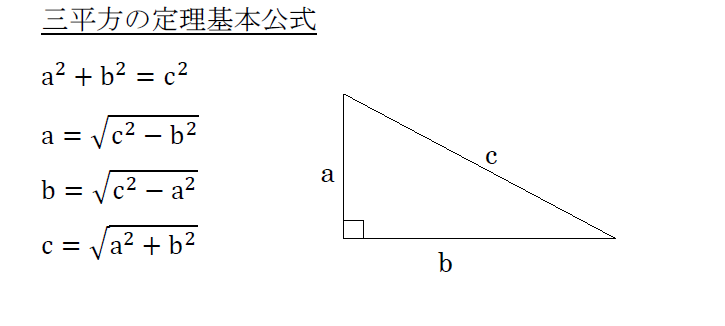三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	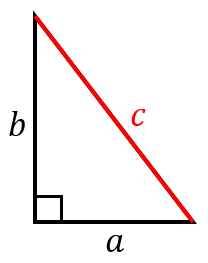三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
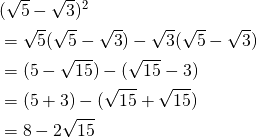三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	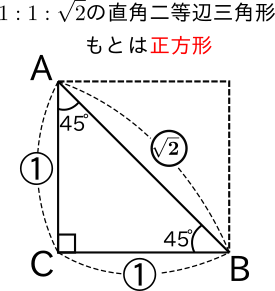三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	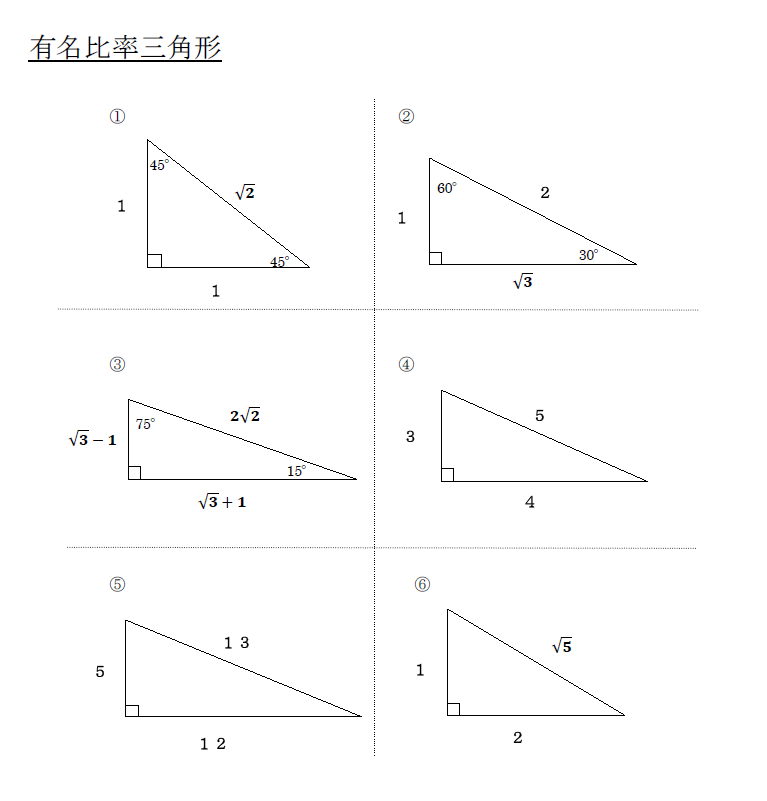三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に	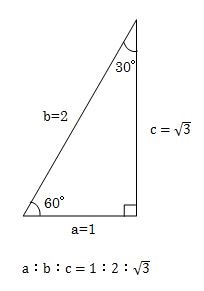三平方の定理 練習問題 苦手な数学を簡単に
三平方の定理 練習問題 苦手な数学を簡単に	三平方の定理 練習問題 苦手な数学を簡単に

 中学校で勉強する三平方の定理は、直角三角形の各辺の長さの関係を表した公式です。 シンプルにして美しい公式です。 この三平方の定理の証明方法は非常に多くあり、100種類以上あると言われています。 興味のある人は以下の記事をご覧ください。 今回は”中学数学の復習方法”をメインに記事にしました。 fapaw 中学数学に中身はない 文字式の計算、連立方程式、三平方の定理だけ復習すればいい。 中学数学は1週間で終わる なぜ数学を嫌いになるの

Incoming Term: 三平方の定理 ルートの計算,